When comparing two values, it is important to understand their relative difference. One way to express this difference is through a percentage. Calculating the percentage difference between two values is an important concept in many fields, including finance, science, and statistics. In this blog post, we’ll take a closer look at percentage difference, explain how to calculate it, and provide some examples.
Check out our Math Calculators
What is Percentage Difference?
Percentage difference is a measure of the relative difference between two values, expressed as a percentage. It tells you how much one value differs from another. One can determine the percentage difference by using the following formula:

Percentage Difference = |(Value 1 – Value 2) / ((Value 1 + Value 2) / 2)| x 100%
In this formula, “Value 1” and “Value 2” are the two values you’re comparing. The vertical bars around the numerator indicate that you should take the absolute value of the difference between the two values, so that the result is always positive.
Let’s take a closer look at each element of the formula:
Value 1: The first value that you are comparing.
Value 2: The second value that you are comparing.
(Value 1 – Value 2): This is the difference between the two values.
(Value 1 + Value 2) / 2: This is the average of the two values.
|(Value 1 – Value 2) / ((Value 1 + Value 2) / 2)|: This is the absolute value of the difference between the two values, divided by their average, and then multiplied by 100%. The vertical bars indicate that you should take the absolute value of this quantity.
Examples of Percentage Difference
Let’s take a look at some examples to illustrate how to calculate percentage difference.
Example 1: Calculating the percentage difference between two prices
Suppose you are considering two phones: Phone A costs $500, while Phone B costs $450. What is the percentage variance between the two prices?
Percentage Difference = |($500 – $450) / (($500 + $450) / 2)| x 100%
Percentage Difference = |$50 / $475| x 100%
Percentage Difference = 10.53%
So, the percentage difference between the two prices is 10.53%.
Example 2: Calculating the percentage difference between two scientific measurements
Suppose you measure the temperature of a sample at two different times and obtain the following values: 25.6°C and 26.2°C. What is the percentage difference between the two temperature measurements?
Percentage Difference = |(25.6 – 26.2) / ((25.6 + 26.2) / 2)| x 100%
Percentage Difference = |-0.6 / 25.9| x 100%
Percentage Difference = 2.31%
So, the percentage difference between the two temperature measurements is 2.31%.
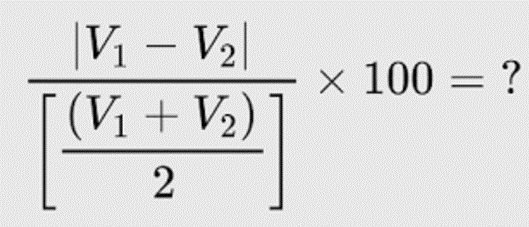
Example 3: Calculating the percentage difference between two distances
Suppose you run a 5K race in two different locations, and you finish in 25 minutes in the first location and 27 minutes in the second location. What is the percentage difference between your finish times?
Percentage Difference = |(25 – 27) / ((25 + 27) / 2)| x 100%
Percentage Difference = |-2 / 26| x 100%
Percentage Difference = 7.69%
So, the percentage difference between your finish times is 7.69%.
Using Percentage Difference in Data Analysis
Percentage difference is a useful tool for data analysis, especially when you are comparing data over time. For example, suppose you are analyzing sales data for a company over two years. You want to determine the percentage difference in sales between the two years to understand the growth or decline in the company’s sales.
Let’s say that the company’s sales in the first year were $1,000,000, while the sales in the second year were $1,500,000. You can use the formula for percentage difference to calculate the percentage change in sales between the two years.
Percentage Difference = |($1,500,000 – $1,000,000) / (($1,500,000 + $1,000,000) / 2)| x 100%
Percentage Difference = |$500,000 / $1,250,000| x 100%
Percentage Difference = 40%
In this example, the percentage difference between the two years is 40%, which means that the company’s sales grew by 40% from the first year to the second year.
Find out what is 2/3 as a percentage
Using Percentage Difference for Statistical Analysis
Percentage difference is also useful for statistical analysis. For example, you can use percentage difference to compare the means of two different data sets. Let’s say that you want to compare the mean score of two different classes on a test. The mean score of Class A is 80, while the mean score of Class B is 75.
You can use the formula for percentage difference to calculate the percentage difference between the mean scores of the two classes.
Percentage Difference = |(80 – 75) / ((80 + 75) / 2)| x 100%
Percentage Difference = |5 / 77.5| x 100%
Percentage Difference = 6.45%
In this example, the percentage difference between the mean scores of the two classes is 6.45%, which means that Class A has a slightly higher mean score than Class B.
Using Percentage Difference in Finance
Percentage difference is an important tool in finance for calculating returns and evaluating investment opportunities. For example, let’s say that you invest $10,000 in a stock and sell it after one year for $12,000. You can use the formula for percentage difference to calculate your return on investment.
Percentage Difference = |($12,000 – $10,000) / (($12,000 + $10,000) / 2)| x 100%
Percentage Difference = |$2,000 / $11,000| x 100%
Percentage Difference = 18.18%
In this example, the percentage difference between the initial investment and the selling price is 18.18%, which means that you earned an 18.18% return on your investment.
Limitations of Percentage Difference
While percentage difference is a useful tool, it is important to be aware of its limitations. One of the limitations of percentage difference is that it does not take into account the magnitude of the values being compared. For example, a 10% difference between two small values may not have the same significance as a 10% difference between two large values.
Another limitation of percentage difference is that it assumes that the two values being compared are independent of each other. If the two values are related, such as in a before-and-after experiment, percentage difference may not be the most appropriate tool for analysis.

Summary
Percentage difference is a valuable tool for comparing two values and understanding their relative difference. It can be used in a wide range of fields, including finance, science, and statistics, and it can help you make informed decisions and evaluate data over time. By using the formula for percentage difference, you can easily calculate the percentage difference between two values and gain a better understanding of the data you are working with. It is a simple and effective way to quantify the change in a value over time or to compare two different values.
However, it is important to keep in mind the limitations of percentage difference. It should be used as a complementary tool in data analysis and should not be relied upon as the sole method of analysis. Other tools, such as mean, median, standard deviation, and correlation coefficients, should also be used to gain a more complete understanding of the data.
Additionally, it is important to be aware of the context in which percentage difference is being used. As mentioned earlier, a 10% difference between two small values may not be as significant as a 10% difference between two large values. Therefore, it is important to consider the magnitude of the values being compared and the overall context of the data before making any conclusions based on the percentage difference.
In closing, percentage difference is a valuable tool for data analysis, finance, and statistics. It allows you to easily compare two values and quantify the change between them over time. By being aware of its limitations and using it in conjunction with other analytical tools, you can gain a more comprehensive understanding of the data you are working with and make more informed decisions.